 発電工学
発電工学 【燃料電池】発電原理とギブスの自由エネルギーから考える理論出力
燃料電池とは酸素と水素の化学反応により、水を生成したときの差分の電気エネルギーを動力として取り出す発電装置です。酸素は大気中に存在しており、容易に取り出すことができます。燃料となる水素をタンクに貯めておいて発電が必要な時に供給すれば、発電することができます。
 発電工学
発電工学 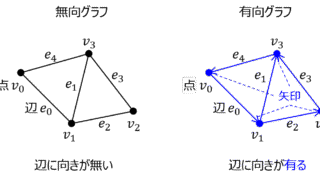 情報
情報 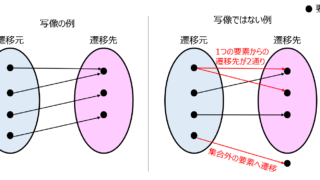 情報
情報 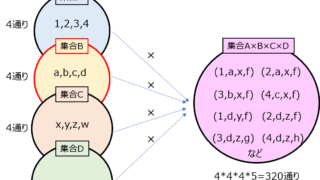 情報
情報 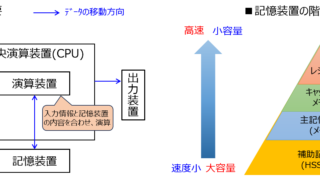 情報
情報 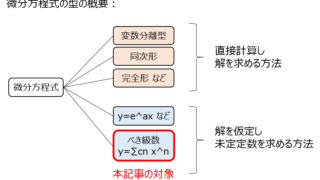 数学
数学 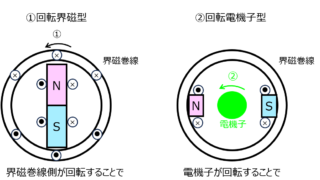 電気機器学
電気機器学 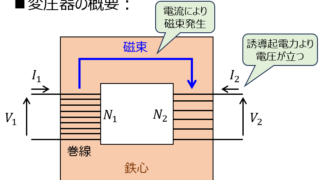 電気機器学
電気機器学 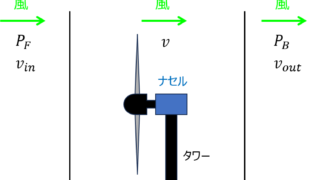 発電工学
発電工学  発電工学
発電工学