 東京科学大学(東工大)
東京科学大学(東工大) 【東工大院】工学院 電気電子系 院試対策(電磁気学/電気回路/量子力学)
東工大(東京科学大学) 電気電子系 院試の全体電気数学、電磁気学、電気回路(電子回路有)、量子力学/物性基礎で構成されています。試験時間は160分(9:30-12:10)です。英語はTOEICによる点数換算で、全科目合わせて合計950点満点になっています。
 東京科学大学(東工大)
東京科学大学(東工大)  東京科学大学(東工大)
東京科学大学(東工大) 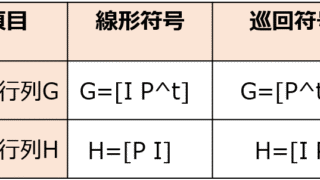 通信
通信 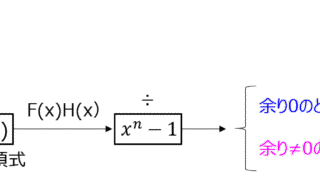 通信
通信  通信
通信 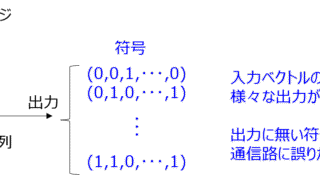 通信
通信 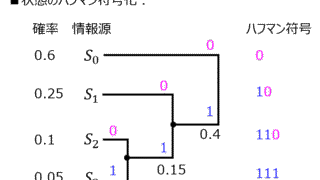 通信
通信 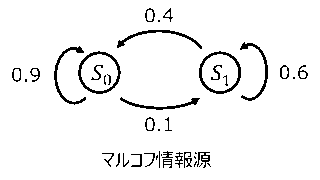 通信
通信 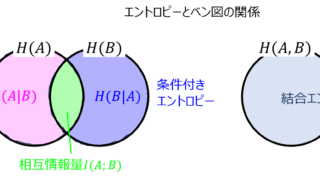 通信
通信 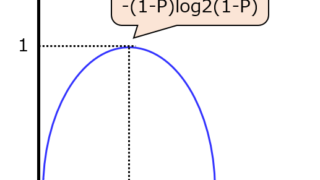 通信
通信