 通信
通信 パルス幅変調信号(APM)の原理と復元方法、問題
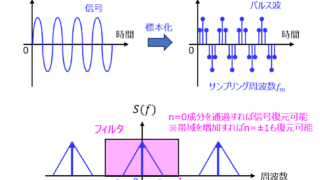
パルス幅変調(PAM)とはある周波数以下の信号を標本化し、周期Tごとに波形を持つ信号に変換することを言います。(PAM:Pulse Amplitude. Modulationの略です。)標本化した後の信号は、Tごとに決まった波形が出るため、帯域幅が\(\dfrac{1}{2T}\)の低域通過フィルタを用いれば、\(t=0\)の波形のみ復元できます。
 通信
通信  通信
通信  通信
通信  通信
通信  発電工学
発電工学 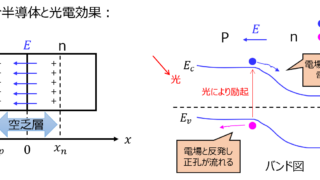 半導体デバイス
半導体デバイス 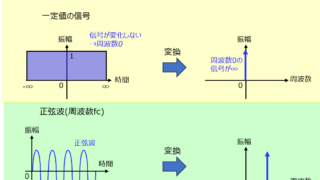 通信
通信 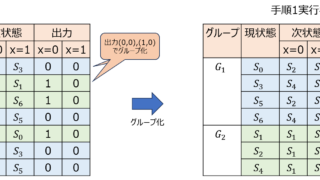 情報
情報 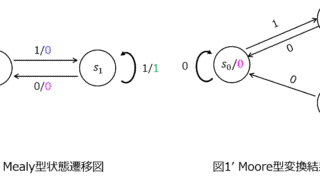 情報
情報  情報
情報