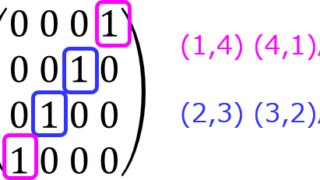 数学
数学 【線形代数】行列のn乗の計算問題
行列のn乗を求めるには、固有値を用いて対角化を行うことが多いです。この方法については、イレギュラーケースも含めてこちら1、こちら2の記事で説明しています。本問も上記の考え方で解くこともできます。しかし、nをある値にして計算(実験)し、規則性を見つけることで答えを出すことも可能です。また、そのほうが時間がかからないケースもあり、本問がそれに該当します。
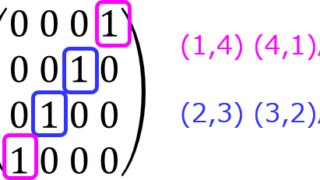 数学
数学  数学
数学  制御工学
制御工学  制御工学
制御工学  制御工学
制御工学  電磁気学
電磁気学 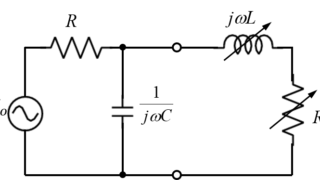 電気回路
電気回路  電気回路
電気回路 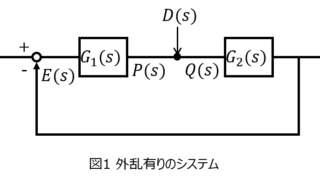 制御工学
制御工学 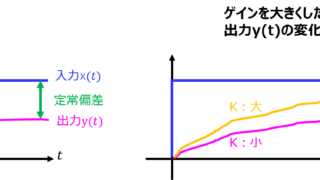 制御工学
制御工学